අපි කලින් Post එකෙන් ඉගෙන ගත්තා Linear Regression ගැන. අද අපි කතා කරන්නේ Cost Function and Gradient Descent ගැන.
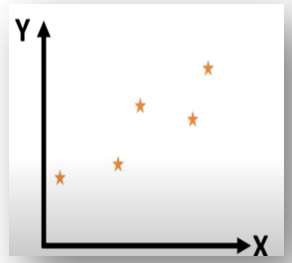
අපි බලමු පහත පෙන්වලා තියන ප්රස්ථාරය
ඒ ප්රස්ථාරයේ data point රාශියක් තියනවා. ඒ හරහා යා හැකි රේඛාවන් ගණනාවක් තියන බව අනිත් ප්රස්ථාරයෙන් පේනවා. නමුත් අපි මේ රේඛා සියල්ලගෙන් ම එක රේඛාවක් එනම් සාධාරණ රේඛාව සොයා ගන්න ඕනි. ඒ රේඛාවට අදාළ අනුක්රමණය හා අන්ත:ඛන්ඩය සොයා ගන්න ඕනි. ඉහත අඳින ලද රේඛා අතරින් එක රේඛාවක් සලකමු. යම් තාක් දුරකට අඳින ලද සාධාරණ රේඛාවක් පහත ප්රස්ථාරයෙන් පෙනෙනවා.
මේ ප්රස්ථාරයේ දකින්නට ලැබෙන සෑම data point එකටම X අගයක් හා Y අගයක් තියනවා. ඒ වගේම ඒ ඒ ලක්ෂ වල ඉඳලා රේඛාවට සම්බන්ධ වන තැන් වලටත් X අගයක් හ ා Y අගයක් තියනවා. ඒ ඒ ලක්ෂ වල එකම X අගයට Y අගය හා රේඛාව මත ඇති Y අගය අතර වෙනස් කමක් තියනවා.
රූප සටහනේ පෙන්නුම් කරන ආකාරයට සෑම X අගයකටම Y actual හා Y predicted අගයක් තියනවා මේ අගයන් අතර පරතරය අඩු වන තරමට තමයි මේ රේඛාව සාධාරඛ රේඛාව කියලා කියන්න පුළුවන්
මේ සියලුම ලක්ෂ වල Y actual හා Y predicted අගයන් අතර වෙනස හී එකතුව අරගෙන වර්ග කරලා තියන ලක්ෂ ගණනින් බෙදුවම අපිට cost function එක නැත්නම් error එක ලැබෙනවා. මේ error එක අඩුවෙන තරමට තමයි අපිට සාධාරණ රේඛාව ලැබෙන්නේ.
ඉහත ප්රස්ථාර දෙක අනුක්රමණය හා අන්ත:ඛන්ඩය cost එකට එරෙහිව අඳින ලදි. එහි දී එම ප්රස්ථාර වල අවම cost එකේ m හා c අගය ගන්නවා. මෙම ප්රස්ථාර දෙකම එකම ප්රස්ථාරයක් විදියට ගත්තොත් පහත ආකාරයට පෙන්නනවා.
දැන් අපි බලමු Gradient Descent Algorithm එක python භාවිතා කරලා කරන්නේ කොහොම ද කියලා.
අපි cost function එක අවම වන සාධාරණ රේඛාව ගන්න ඕනි. ඒක කරන්න අපි Gradient descent algorithm එක භාවිතා කරනවා.
අපිට මෙතන දී සොයා ගන්න ඕනි parameters දෙකක් තියනවා. එනම් සාධාරණ රේඛාවේ අනුක්රමණය හා අන්ත:ඛන්ඩය.
ඉහත ප්රස්ථාර දෙක අනුක්රමණය හා අන්ත:ඛන්ඩය cost එකට එරෙහිව අඳින ලදි. එහි දී එම ප්රස්ථාර වල අවම cost එකේ m හා c අගය ගන්නවා. මෙම ප්රස්ථාර දෙකම එකම ප්රස්ථාරයක් විදියට ගත්තොත් පහත ආකාරයට පෙන්නනවා.
import numpy as np
import matplotlib.pyplot as plt
n=5 # number of data points
#simple data set
x=np.array([1,2,3,4,5])
y=np.array([5,8,11,14,17])
m=c=0 #start with m=0 and c=0
learning_rate=0.01
for i in range(1,101):
y_predict=m*x+c
cost=(1/n)*sum([value**2 for value in (y-y_predict)])
plt.scatter(m, cost)
dm=-(2/n)*sum(x*(y-y_predict))
dc=-(2/n)*sum(y-y_predict)
m=m -learning_rate*dm
c=c -learning_rate*dc
print("m {},c {},cost {},iteration {}".format (m,c,cost,i))
plt.show()
output
m 0.78,c 0.22,cost 139.0,iteration 1
m 1.3752,c 0.38880000000000003,cost 81.09039999999999,iteration 2
m 1.829328,c 0.5185120000000001,cost 47.342957440000006,iteration 3
m 2.1757651200000003,c 0.6183820800000001,cost 27.676028061184002,iteration 4
m 2.4399938688000002,c 0.6954685312000001,cost 16.214528671342176,iteration 5
m 2.641467105792,c 0.755159528448,cost 9.53475161511504,iteration 6
m 2.7950347708108803,c 0.8015683115315201,cost 5.641529540691357,iteration 7
m 2.9120330225405953,c 0.8378348590522369,cost 3.3721776630341185,iteration 8
m 3.00111566603853,c 0.8663561805187564,cost 2.04914082373806,iteration 9
m 3.068888848678928,c 0.8889621169460694,cost 1.277573393810718,iteration 10
m 3.1203955749527994,c 0.9070495436864123,cost 0.8273788621627981,iteration 11
m 3.1594855758419986,c 0.9216848183155161,cost 0.5644683476096531,iteration 12
m 3.189097660057828,c 0.9336819873986858,cost 0.4107014628287187,iteration 13
m 3.2114752556011847,c 0.9436624880472424,cost 0.3205418330682894,iteration 14
m 3.2283309500860895,c 0.9521007229502264,cost 0.2674530881580191,iteration 15
m 3.240972097690136,c 0.9593588514860565,cost 0.23597112014101074,iteration 16
m 3.250396705109143,c 0.9657133485949272,cost 0.217084187496984,iteration 17
m 3.257366629069436,c 0.97137527931648,cost 0.20554066859819098,iteration 18
m 3.262463453915171,c 0.9765057759859843,cost 0.1982801537066147,iteration 19
m 3.2661311474946744,c 0.9812278532313543,cost 0.19351916306026645,iteration 20
m 3.268708623851965,c 0.9856354273170468,cost 0.19021834863583312,iteration 21
m 3.2704546009655098,c 0.989800201339588,cost 0.1877720057119176,iteration 22
m 3.2715665766727224,c 0.9937769212548657,cost 0.18582713557824082,iteration 23
m 3.2721953145294314,c 0.9976073882294051,cost 0.18417800423907482,iteration 24
m 3.272455902039192,c 1.0013235215930512,cost 0.1827046964445598,iteration 25
m 3.272436192294987,c 1.0049496970388385,cost 0.1813373080210592,iteration 26
m 3.2722032481677594,c 1.0085045315603625,cost 0.18003507893292925,iteration 27
m 3.2718082616772306,c 1.0120022460390896,cost 0.1787742330629022,iteration 28
m 3.2712903093458947,c 1.015453705417674,cost 0.1775408918370407,iteration 29
m 3.2706792189647373,c 1.0188672127485667,cost 0.17632694463513032,iteration 30
m 3.269997758027581,c 1.0222491153557112,cost 0.17512764226924626,iteration 31
m 3.2692633043401704,c 1.0256042675669421,cost 0.1739401945811601,iteration 32
m 3.2684891213313163,c 1.028936383955193,cost 0.17276295319050045,iteration 33
m 3.267685331601115,c 1.0322483089962102,cost 0.17159493523981642,iteration 34
m 3.2668596601090973,c 1.0355422229202191,cost 0.17043554585574697,iteration 35
m 3.2660180015098828,c 1.038819798855269,cost 0.1692844164121298,iteration 36
m 3.2651648532463926,c 1.0420823227875706,cost 0.16814131027672669,iteration 37
m 3.264303646164932,c 1.0453307851370357,cost 0.16700606788409167,iteration 38
m 3.263436996900425,c 1.048565950664399,cost 0.16587857472575618,iteration 39
m 3.2625669005424673,c 1.0517884118370855,cost 0.16475874269550966,iteration 40
m 3.2616948777128996,c 1.0549986295677958,cost 0.1636464992173721,iteration 41
m 3.2608220868419937,c 1.058196964313666,cost 0.16254178090893887,iteration 42
m 3.2599494098779354,c 1.061383699816873,cost 0.16144452988772562,iteration 43
m 3.2590775177157774,c 1.0645590612278595,cost 0.16035469161772756,iteration 44
m 3.2582069201446346,c 1.0677232289403555,cost 0.15927221365354627,iteration 45
m 3.2573380039763937,c 1.0708763491528703,cost 0.1581970449075789,iteration 46
m 3.2564710621524147,c 1.0740185419312294,cost 0.15712913522203756,iteration 47
m 3.2556063159630098,c 1.0771499073634598,cost 0.15606843511859633,iteration 48
m 3.25474393200934,c 1.0802705302584101,cost 0.15501489565158275,iteration 49
m 3.2538840351517804,c 1.0833804837326815,cost 0.15396846832149005,iteration 50
m 3.2530267183944277,c 1.086479831948921,cost 0.15292910502366938,iteration 51
m 3.2521720504307186,c 1.089568632206277,cost 0.1518967580175108,iteration 52
m 3.251320081403584,c 1.0926469365363083,cost 0.1508713799075898,iteration 53
m 3.250470847302617,c 1.095714792921367,cost 0.14985292363177324,iteration 54
m 3.249624373320759,c 1.0987722462247826,cost 0.14884134245339983,iteration 55
m 3.248780676416705,c 1.1018193389010413,cost 0.14783658995583876,iteration 56
m 3.2479397672709673,c 1.1048561115380182,cost 0.14683862003843504,iteration 57
m 3.2471016517790736,c 1.1078826032709999,cost 0.14584738691327812,iteration 58
m 3.2462663321914174,c 1.1108988520988354,cost 0.14486284510244218,iteration 59
m 3.2454338079833756,c 1.1139048951253736,cost 0.14388494943552496,iteration 60
m 3.2446040765195105,c 1.1169007687438637,cost 0.1429136550473515,iteration 61
m 3.2437771335605863,c 1.1198865087778158,cost 0.1419489173757861,iteration 62
m 3.2429529736505884,c 1.1228621505886243,cost 0.14099069215961121,iteration 63
m 3.2421315904121415,c 1.1258277291578165,cost 0.14003893543645746,iteration 64
m 3.2413129767720013,c 1.1287832791499317,cost 0.13909360354075603,iteration 65
m 3.240497125133165,c 1.131728834960613,cost 0.1381546531017248,iteration 66
m 3.239684027506232,c 1.1346644307534108,cost 0.13722204104136537,iteration 67
m 3.238873675609656,c 1.1375901004879687,cost 0.13629572457248587,iteration 68
m 3.2380660609462537,c 1.14050587794163,cost 0.1353756611967331,iteration 69
m 3.23726117486158,c 1.1434117967260222,cost 0.13446180870263932,iteration 70
m 3.2364590085884712,c 1.146307890299807,cost 0.13355412516368786,iteration 71
m 3.2356595532810193,c 1.1491941919785025,cost 0.13265256893638785,iteration 72
m 3.234862800040485,c 1.1520707349420714,cost 0.13175709865836185,iteration 73
m 3.2340687399350543,c 1.1549375522408007,cost 0.13086767324644993,iteration 74
m 3.2332773640148944,c 1.1577946767998815,cost 0.1299842518948235,iteration 75
m 3.232488663323625,c 1.1606421414229902,cost 0.12910679407311393,iteration 76
m 3.231702628907048,c 1.163479978795113,cost 0.12823525952455217,iteration 77
m 3.230919251819791,c 1.1663082214847877,cost 0.12736960826412283,iteration 78
m 3.23013852313035,c 1.1691269019459045,cost 0.126509800576728,iteration 79
m 3.2293604339249184,c 1.1719360525191653,cost 0.1256557970153674,iteration 80
m 3.2285849753102864,c 1.174735705433287,cost 0.12480755839932754,iteration 81
m 3.2278121384160263,c 1.1775258928060042,cost 0.12396504581238298,iteration 82
m 3.2270419143961404,c 1.1803066466449226,cost 0.12312822060101303,iteration 83
m 3.226274294430294,c 1.1830779988482556,cost 0.12229704437262717,iteration 84
m 3.225509269724734,c 1.1858399812054727,cost 0.12147147899380305,iteration 85
m 3.224746831512964,c 1.1885926253978794,cost 0.12065148658853844,iteration 86
m 3.223986971056239,c 1.191335962999144,cost 0.11983702953651353,iteration 87
m 3.223229679643918,c 1.1940700254757868,cost 0.11902807047136187,iteration 88
m 3.222474948593709,c 1.196794844187636,cost 0.11822457227896091,iteration 89
m 3.221722769251835,c 1.1995104503882608,cost 0.1174264980957258,iteration 90
m 3.2209731329931355,c 1.2022168752253855,cost 0.1166338113069184,iteration 91
m 3.2202260312211224,c 1.2049141497412896,cost 0.11584647554496919,iteration 92
m 3.219481455367998,c 1.2076023048731965,cost 0.11506445468780638,iteration 93
m 3.2187393968946467,c 1.2102813714536527,cost 0.1142877128572021,iteration 94
m 3.217999847290605,c 1.2129513802109009,cost 0.1135162144171221,iteration 95
m 3.217262798074018,c 1.2156123617692465,cost 0.11274992397209356,iteration 96
m 3.216528240791579,c 1.2182643466494205,cost 0.11198880636558176,iteration 97
m 3.2157961670184663,c 1.2209073652689373,cost 0.11123282667837378,iteration 98
m 3.2150665683582673,c 1.2235414479424507,cost 0.11048195022698054,iteration 99
m 3.2143394364429017,c 1.2261666248821057,cost 0.10973614256204317,iteration 100
මේ තියෙන්නේ best fit line එකේ m හා c. දැන් cost function හා gradient descent ගැන තෙරෙනවා ඇති කියලා හිතනවා. නමුත් අපිට ඇත්තටම machine learning model එකක් හදන කොට ඕනි වෙන්නේ නැහැ. ඒකට හේතුව machine learning libraries හරහා internally වෙන නිසා. මෙකෙන් අපි ඉගෙන ගත්තේ best fit line එක සොයන ආකාරයයි.
ඉතින් මම ඊළඟ Post එකෙන් අළුත් දෙයක් අරගෙන එන්නම්.











0 Comments